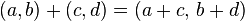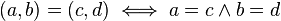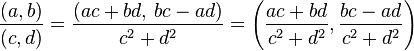Historia de los números complejos
Los números complejos es un tema que ha sido muy poco estudiado por los profesores en las distintas etapas de la educación, tanto a nivel básico y diversificado como en la Universidad. Al comenzar a estudiar los números complejos, nos damos cuenta que es un sistema muy importante por integrar varias ramas de la matemática como lo son la trigonometría, la geometría y el álgebra, entonces resulta bastante interesante indagar un poco más acerca de este tema, comenzando por su historia.
Isaac Asimov, en su libro “De los números y su historia”, relata una historia en la que un profesor de Sociología en su clasificación de la humanidad agrupó a los matemáticos entre los místicos junto con los poetas y los teólogos, ya que para él los matemáticos son místicos porque creen en números que no tienen realidad, para explicarlo dijo lo siguiente, “La raíz cuadrada de menos uno. No tiene existencia. Los matemáticos lo llaman imaginario. Pero de alguna manera mística creen que tiene alguna clase de existencia”. Pero la verdad es que no hay nada de místico en ellos, son tan reales como cualquier otro.
Los números complejos aparecieron muy temprano en las matemáticas, pero fueron ignorados, por ser para la mayoría un poco extraños y difíciles de representar. Al comienzo los hombres solamente aceptaban los números naturales por ser los más adecuados para contar objetos que comúnmente se consideran como unidades. Pero al medir magnitudes como la longitud o el peso, las fracciones se hicieron imprescindibles. Los egipcios y babilonios se las arreglaron para elaborar métodos que les permitieron operar con fracciones. Pero los griegos descubrieron que habían cantidades definidas que no podían ser expresadas como cocientes de números enteros, la noción de número extiende más allá, ya que los griegos no aceptaban que hubieran números menores que el cero. Los números complejos aparecen entre las soluciones de las ecuaciones cuadráticas, que generan raíces cuadradas de números negativos los cuales no poseen soluciones reales. Los matemáticos griegos que conocían métodos geométricos de resolución, consideraban estos problemas irresolubles, rechazaban el uso de números negativos por la falta de un equivalente dentro de la geometría que para ese momento era el centro de la matemática. El surgimiento de los números complejos no se debió solo a la imposibilidad de resolver algunas ecuaciones cuadráticas, sino que viene también de las ecuaciones cúbicas. Más adelante con el surgimiento del álgebra durante la Edad Media, el concepto de número se amplía para manipular ecuaciones, desligadas de la geometría.
Los números complejos aparecieron muy temprano en las matemáticas, pero fueron ignorados, por ser para la mayoría un poco extraños y difíciles de representar. Al comienzo los hombres solamente aceptaban los números naturales por ser los más adecuados para contar objetos que comúnmente se consideran como unidades. Pero al medir magnitudes como la longitud o el peso, las fracciones se hicieron imprescindibles. Los egipcios y babilonios se las arreglaron para elaborar métodos que les permitieron operar con fracciones. Pero los griegos descubrieron que habían cantidades definidas que no podían ser expresadas como cocientes de números enteros, la noción de número extiende más allá, ya que los griegos no aceptaban que hubieran números menores que el cero. Los números complejos aparecen entre las soluciones de las ecuaciones cuadráticas, que generan raíces cuadradas de números negativos los cuales no poseen soluciones reales. Los matemáticos griegos que conocían métodos geométricos de resolución, consideraban estos problemas irresolubles, rechazaban el uso de números negativos por la falta de un equivalente dentro de la geometría que para ese momento era el centro de la matemática. El surgimiento de los números complejos no se debió solo a la imposibilidad de resolver algunas ecuaciones cuadráticas, sino que viene también de las ecuaciones cúbicas. Más adelante con el surgimiento del álgebra durante la Edad Media, el concepto de número se amplía para manipular ecuaciones, desligadas de la geometría.
DEFINICION
Definiremos cada complejo z como un par ordenado de números reales (a, b) ó (Re(z), Im(z)), en el que se definen las siguientes operaciones:
Suma
Producto por escalar
Multiplicación
Igualdad
A partir de estas operaciones podemos deducir otras como las siguientes:
Resta
División
Al primer componente (que llamaremos a) se le llama parte real y al segundo (que llamaremos b), parte imaginaria. Se denomina número imaginario puro a aquel que está compuesto sólo por la parte imaginaria, es decir, aquel en el que .
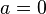
FORMA RECTANGULAR
Sé a visto con anterioridad que los números reales pueden representarse geométricamente como puntos en una línea recta de igual manera trataremos de representar geométricamente él número complejo asignándole a la parte real del número complejo el eje coordenado X y a la parte imaginaria del número complejo el eje coordenado Y
Ejemplos:
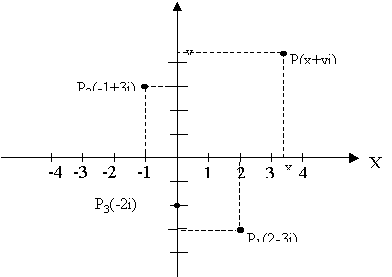
De acuerdo con lo explicado con anterioridad podemos concluir que nosotros podemos graficar cualquier número complejo en los ejes coordenados.
Unidad imaginaria
Tomando en cuenta que  , se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como
, se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como
 , se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como
, se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como
De donde se deduce inmediatamente que,

Conjugado de un número complejo
Se llama conjugado de un número complejo al número complejo que se obtiene por simetría del dado respecto del eje de abscisas.
Representando el número complejo a + bi y haciendo la correspondiente simetría, se tiene que su conjugado es a - bi .
Dado un número complejo, su conjugado puede representarse poniendo encima del mismo una línea horizontal. Así se escribirá:
Propiedades de los conjugados
· Primera propiedad
El conjugado del conjugado de un complejo z es el propio z.
Demostración:
En efecto si z = a + bi se tiene que  = a - bi , de donde,
= a - bi , de donde,  = a + bi = z
= a + bi = z
· Segunda propiedad
Dados dos números complejos cualesquiera z y z' , el conjugado de su suma es igual a la suma de sus conjugados.
Esto se expresa escribiendo que 
Demostración:
Tomando z = a + bi y z' = c + di , se tiene:
Por otra parte:
y es fácil ver que esta expresión coincide con la anterior.
· Tercera propiedad
El conjugado del producto de dos números complejos es igual al producto de los conjugados de dichos números:
Demostración:
Si z = a + bi y z = c + di se tiene que z · z = (ac - bd ) + (ad + bc)i , cuyo conjugado es  = (ac - bd) - (ad + bc)i .
= (ac - bd) - (ad + bc)i .
Calculando por otro lado el producto de los conjugados, resulta que
El resultado es igual al anterior.
· Cuarta propiedad
Los complejos que coinciden con sus conjugados son los números reales.
Demostración:
Sea un complejo a + bi que coincida con su conjugado. Esto equivale a que
a + bi = a - bi
Pero esto sólo ocurre si b = 0, es decir si a + bi es un número real.
· Quinta propiedad
La suma y el producto de un complejo y su conjugado son, ambos, números reales.
Demostración:
(a + bi ) + (a - bi ) = 2a
(a + bi ) (a - bi ) = a2 - (bi )2 = a2 + b2
Operaciones con números complejos
La suma y diferencia de números complejos se realiza sumando y restando las partes reales y las partes imaginarias entre sí, respectivamente.
Suma:
(a + bi) + (c + di) = (a + c) + (b + d)i
Resta:
(a + bi) − (c + di) = (a − c) + (b − d)i
Multiplicación de números complejos
El producto de los números complejos se realiza aplicando la propiedad distributiva del producto respecto de la suma y teniendo en cuenta que i2 = −1.
(a + bi) · (c + di) = (ac − bd) + (ad + bc)i
División de números complejos
El cociente de números complejos se realiza multiplicando numerador y denominador por el conjugado de este.

Igualdad de numerous complejos
Dos números complejos son iguales si lo son las partes reales e imaginarias respectivamente:
Dado el número complejo z = a + b i
· su opuesto como el número complejo − z = − a − b i
· su conjugado como el número complejo z ¯ = a − b i
Observa que el
· opuesto de z es simétrico a z respecto del origen
· conjugado de z es simétrico a z respecto al eje X.